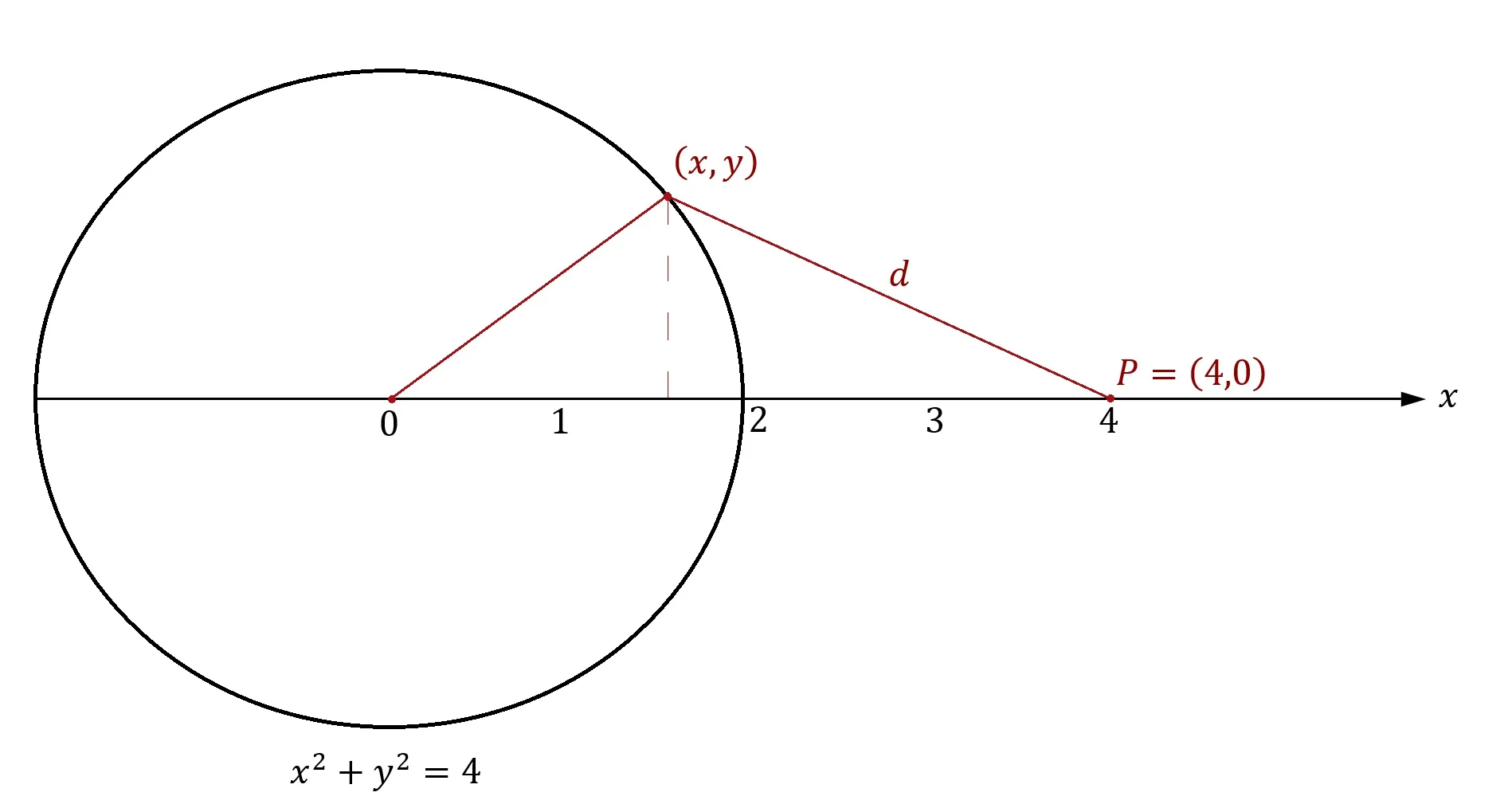
If \((x,y)\) represents any point on the circle, if \(P\) is a point fixed at the coordinate point \((4,0)\), and if \(d\) represents the distance between those two points then, by using only calculus, we can find the point \((x,y)\) on the circle associated with the minimum distance \(d\).

Given that the perimeter \(2x+2y\) of any arbitrary rectangle must be constant, we can use calculus to find that particular rectangle with the greatest area. The solution to this problem has practical applications. For example, suppose that someone had only 30 meters of fencing to enclose their backyard and they wanted to know what fencing layout would maximize the size and total area of their backyard. Using calculus, we can answer such questions.

Calculus—specifically, derivatives—can be used to find the values of \(x\) at which the function \(f(x)\) is at either a minimum value or a maximum value. For example, suppose that we let \(x\) denote the horizontal distance away from the beginning of a hiking trail near a mountain and we let \(f(x)\) denote the altitude of the mountainous terrain at each \(x\) value. \(f(x)\) reaches a minimum value when the function "flattens out"—that is, when \(f'(x)\) becomes equal to zero. These particular values of \(x\) are associated with the bottom and top of the mountain. The condition that \(f'(x)=0\) only tells us that \(f(x)\) is at either a minimum or a maximum. To determine whether or not \(f(x)\) is at a minimum or a maximum, we must use the concept of the second derivative. This will be the topic of discussion in this lesson.

The icy asteroids and comets in the Kuiper belt will one day (perhaps during the 22nd century) be hurled towards Mars’ atmosphere where they’ll disintegrate and release nitrogen into the atmosphere—a crucial step in the project of terraforming Mars. In the future, asteroids will perhaps be used as spaceships powered by nuclear reactors. The fuel for these nuclear reactors—deuterium and helium-3—could be harvested from the asteroids and the atmospheres of gas giants, respectively. As the famous physicist Freeman Dyson once noted, since the Oort Cloud contains all the ingredients necessary to support life, this realm of a trillion or more comets will likely be a way point for a long voyage to the Alpha Centuari star system.

In Carl Sagan's book Pale Blue Dot, he argued that humans evolved a love for exploration as an essential part of our survival as a species. It was this evolutionary trait which compelled our hunter-gather ancestors to leave their home—Africa—when times were getting rough and to meander across the planet. As planetary catastrophes become increasingly likely as time rolls by, Sagan argues that this same "survival strategy" will perhaps compel humanity to colonize the solar system, and beyond. Even the universe itself will one day become too dangerous for humans to live in and we’ll need to voyage to another universe to survive.

In this lesson, we'll use the concept of a definite integral to calculate the arc length of a curve.

The Kardeshev scale ranks how advanced a technological civilization is based on its power consumption. A Type I civilization is a civilization which has harnessed all of their planet's renewable energy sources and who can control the natural forces of their planet such as the weather and volcanoes; a Type II civilization has harnessed the total power output of their home-star and routinely move and dissemble stars; a Type III civilization is one which has spread across the entire galaxy and harnessed the total power output of their galaxy; a Type IV civilization is one with faster-than-light (FTL) speed spacecraft and that has harnessed the total power output of all the galaxies in their universe; Type V civilizations are like gods which have colonized other universes and can spontaneously create other universes at will.

In this lesson, we'll determine the electric potential difference (also called voltage) across any arbitrary capacitor.

In the previous lesson, we defined the concept of a line integral and derived a formula for calculating them. We learned that line integrals give the volume between a surface \(f(x,y)\) and a curve \(C\). In this lesson, we'll learn about some of the applications of line integral for finding the volumes of solids and calculating work. In particular, we'll use the concept of line integrals to calculate the volume of a cylinder, the work done by a proton on another proton moving in the presence of its electric field, and the work done by gravity on a swinging pendulum.

Line integrals are used to find the area between a surface \(f(x,y)\) and any arbitrary curve. In this lesson, we'll define the idea of line integral and derive a formula for calculating them.