Gravitational force exerted by ring
force exerted by a disk of mass \(M\) on a particle of mass \(m\) a vertical height \(h\) above the center \(O\) of the disk as illustrated in Figure 2. To find this force we'll use Newton's law of gravity and the concept of a definite integral just like we did in the previous lesson. Let's say that the radius of the disk is \(R\) and that the disk has a finite thickness \(t\). Let's imagine subdividing this disk into infinitely many, infinitesimally skinny rings. I have drawn one of these rings in Figure 1. If the entire disk has a uniform mass density \(ρ\), then since the volume of one of the infinitesimal mass elements comprising the ring is \(dV\) it follows that the mass of such a mass element must be
$$dm=ρdV.\tag{1}$$
Figure 1: A ring of mass \(M=\int{dm}\) exerts a gravitational force on a particle of mass \(m\) a horizontal distance \(h\) away from the center of the ring. The vertical component of force \(dF_y\) for every mass element \(dm\) in the ring is canceled out by the vertical component of force \(dF'_y\) for another mass element \(dm'\) located on the opposite side of the ring.
Since all of the mass of each mass element is contained within an infinitesimally small volume \(dV\), we can regard each mass element as a point-mass (that is, a particle). This is nice since, as we explained in another lesson, Newton's law of gravity tells us the gravitational force that one particle exerts on another particle. Using Newton's law of gravity, we find that the point-mass \(ρdV\) exerts a gravitational force on the particle of mass \(m\) by an amount given by
$$dF_{ρdV,m}=G\frac{(ρdV)(m)}{r^2+h^2}.\tag{2}$$
To find the total gravitational force exerted by the entire ring, we must add up every force \(dF_{ρdV,m}\) due to all the particles comprising the ring. But notice that when we take this sum, all of the \(y\)-components of force cancel each other out. Let me take a moment to explain why this is. Notice that for any arbitrary mass element \(dm\) comprising the ring, there will always be some other mass element \(dm'\) on the opposite side of the ring. Since each mass element is an equal distance \(\sqrt{r^2+h^2}\) away from \(m\), both mass elements will exert the same magnitude of force on \(m\). But, due to their symmetrical distribution around \(m\), there \(y\)-components of force acting on \(m\) will be equal-and-opposite. Thus, the two \(y\)-components of force exerted by the particles \(dm\) and \(dm'\) cancel each other out. When we add up the forces exerted by each particle in each ring comprising the disk, the \(y\)-components of force always cancel. Thus, we really only need to add up the \(x\)-components of force exerted by each particle in the ring. As you can see from Figure 1, \(cosθ=dF_x/dF_{ρdV,m}\) and thus
$$dF_x=dF_{ρdV,m}cosθ.\tag{3}$$
Substituting Equation (3) into (2), we find that the \(x\)-component of gravitational force exerted by any arbitrary mass element in the ring is given by
$$dF_x=\frac{Gρm}{r^2+h^2}cosθdV.\tag{4}$$
To find the total gravitational force exerted by the ring on \(m\), we must add up the forces due to every particle in the ring to get
$$F_{ring}=\int{\frac{Gρm}{r^2+h^2}cosθdV}.\tag{5}$$
We know that the terms \(G\), \(ρ\), and \(m\) are all constants; but notice that for any particle along the ring, \(r\) and \(θ\) are also constants. Thus, we can pull everything outside of the integral in Equation (5). Doing so, we have
$$F_{ring}=\frac{Gρm}{r^2+h^2}cosθ\int{dV}.$$
Since \(\int{dV}=ΔV\), which is the volume of the ring, we have
$$F_{ring}=\frac{Gρm}{r^2+h^2}cosθΔV.$$
Since \(ρΔV\) is just the mass of the ring (which we'll represent by \(M_{ring}\), we find that the total gravitational force exerted by a ring on a particle a height \(h\) above or below the center of the ring is given by
$$F_{ring}=G\frac{mM_{ring}}{r^2+h^2}cosθ.\tag{7}$$
Gravitational force exerted by disk
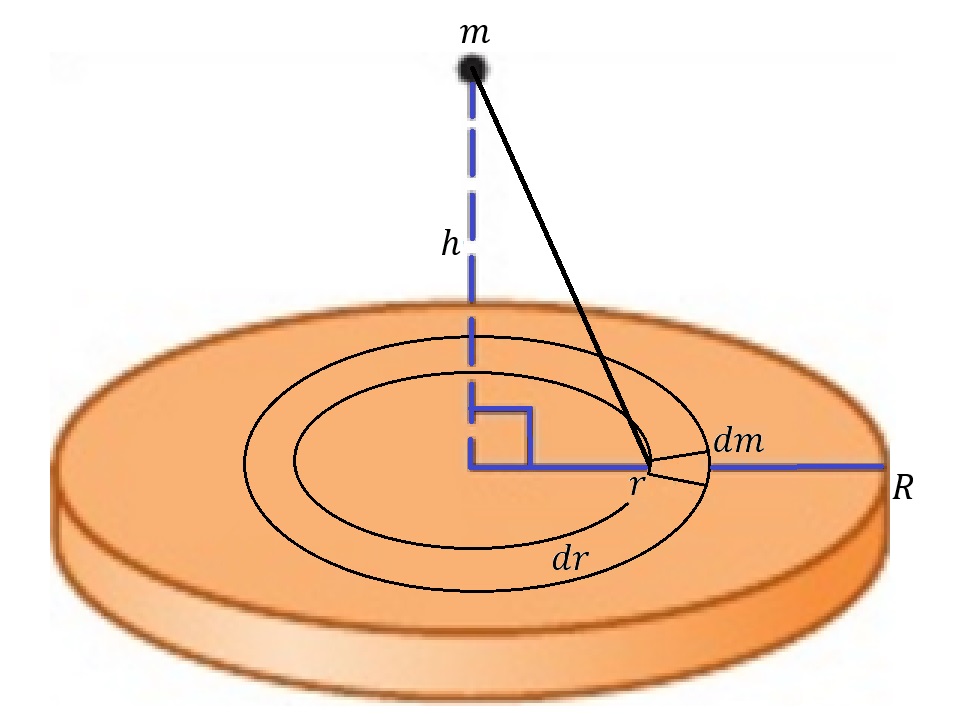
Figure 2: A disk of mass \(M=\int{m_{ring}}\) exerts a gravitational force on a particle of mass \(m\) a distance \(h\) away from the center of the disk along the \(x\)-axis. By summing the gravitational force exerted on \(m\) by each ring of radius \(r\) from \(r=0\) to \(r=R\), we can find the total gravitational force exerted on \(m\) by the entire disk.
To find the gravitational force exerted on \(m\) by the disk, all that we need to do is sum up the forces exerted by every ring comprising the disk to get
$$F_{disk}=\int{\frac{GρmcosθdV}{r^2+h^2}},\tag{8}$$
where I have set \(ΔV=dV\) since the ring is infinitesimally skinny. The rest of this lesson will be about simplifying the integral in Equation (8) so that we can eventually solve it. To solve this integral, everything in the integral must be represented in terms of a single variable. Let's represent everything in terms of \(r\). The volume \(dV\) of the ring is given by
$$dV=(2πrdr)t.$$
Substituting this result into Equation (8), we have
$$F_{disk}=\int{\frac{Gρmcosθ}{r^2+h^2}(2πrdr)t},\tag{9}$$
Substituting \(cosθ=h/\sqrt{r^2+h^2}\) and rearranging the terms in Equation (9), we have
$$F_{disk,m}=2πhGρmt\int_0^R\frac{r}{(r^2+h^2)^{3/2}}dr.\tag{11}$$
Now that we have simplified our integral so that everything is in terms of the single variable \(r\), we can compute the integral using the fundamental theorem of calculus and u-substitution. If we let \(u=r^2+h^2\), then
$$\frac{du}{dr}=2r$$
and
$$rdr=\frac{1}{2}du.\tag{12}$$
Substituting Equation (12) into (11), we have
$$hπGρmt\int_{h^2}^{R^2+h^2}\frac{1}{u^{3/2}}du.\tag{14}$$
Using the rules of integration and the fundamental theorem of calculus to solve the integral in Equation (14), Equation (14) becomes
$$2hπGρmt\biggl[\frac{1}{\sqrt{u}}\biggr]_{R^2+h^2}^{h^2}=2hπGρmt\biggl(\frac{1}{h}-\frac{1}{\sqrt{R^2+h^2}}\biggr).$$
Multiply by \(h/h\), we have
$$2hπGρmt\biggl(\frac{1}{h}-\frac{1}{\sqrt{R^2+h^2}}\biggr)=2πGρmt\biggl(1-\frac{h}{\sqrt{R^2+h^2}}\biggr).$$
Thus, the gravitational force exerted by a disk on a particle of mass \(m\) located a vertical distance \(h\) above or below the center of the disk is given by
$$F_{disk}=2πGρmt\biggl(1-\frac{h}{\sqrt{R^2+h^2}}\biggr).\tag{15}$$
This article is licensed under a CC BY-NC-SA 4.0 license.